61. Autograd

import torch
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt

row = 5
col = 3

tensor_1 = torch.ones(row,col)

x1 = Variable( tensor_1, requires_grad=True )
print(x1)

tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]], requires_grad=True)

Variable is used to specify a computation graph, and also the accumulatioin of gradients.

They keep track of what created them.

x2 = x1 + 1
print(x2)

tensor([[2., 2., 2.],
        [2., 2., 2.],
        [2., 2., 2.],
        [2., 2., 2.],
        [2., 2., 2.]], grad_fn=<AddBackward0>)

print( x2.grad_fn, x2._version )

<AddBackward0 object at 0x7f1c1983ebb0> 0

61.1. Autograd

Backprop is basically chain rule of derivatives.

Autograd does it.

tensor_3 = torch.Tensor( np.linspace(0,2*np.pi,10) )
print(tensor_3)
x_3 = Variable( tensor_3, requires_grad=True )
print(x_3)
y_3 = torch.sin(x_3)
print(x_3)

tensor([0.0000, 0.6981, 1.3963, 2.0944, 2.7925, 3.4907, 4.1888, 4.8869, 5.5851,
        6.2832])
tensor([0.0000, 0.6981, 1.3963, 2.0944, 2.7925, 3.4907, 4.1888, 4.8869, 5.5851,
        6.2832], requires_grad=True)
tensor([0.0000, 0.6981, 1.3963, 2.0944, 2.7925, 3.4907, 4.1888, 4.8869, 5.5851,
        6.2832], requires_grad=True)

print(x_3.grad)

None

y_3.backward( torch.Tensor( np.ones(10) ) )

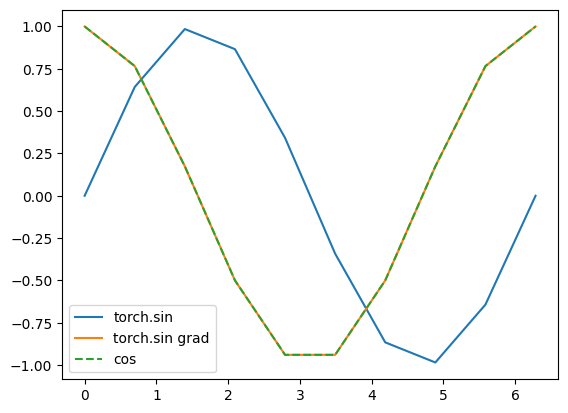
plt.plot(x_3.data.numpy(), y_3.data.numpy(), label="torch.sin" )
plt.plot( x_3.data.numpy(), x_3.grad.data.numpy() , label="torch.sin grad" )
plt.plot( x_3.data.numpy(), np.cos(x_3.data.numpy() ) , '--',label="cos")
plt.legend()

<matplotlib.legend.Legend at 0x7f1c197d7370>